Содержание
Математически набор — это коллекция или список объектов. Наборы состоят не только из цифр, но могут содержать что угодно, включая еду в вашем холодильнике, планеты в солнечной системе или корабли с именем Enterprise.
Примеры наборов
Хотя наборы могут содержать что угодно, наборы часто ссылаются на числа, которые соответствуют шаблону или связаны каким-либо образом, например:
- Множество положительных четных чисел меньше 10, например, равно 0, 2, 4, 6, 8
- Набор коэффициент для числа 12, например, составляет 1, 2, 3, 4, 6, 12
- Например, набор простых чисел меньше 50 равен 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Установить обозначение
Объекты в наборе называются элементами, а наборы используют следующие обозначения или соглашения:
- Одиночные, заглавные буквы, такие как J, E или F, обозначают наборы
- Строчные буквы или цифры являются элементами набора
- Фигурные скобки {} обозначают список элементов в наборе
- Запятые отдельные элементы набора
Итак, примеры обозначений набора будут:
- J = {Юпитер, Сатурн, Уран, Нептун}
- E = {0, 2, 4, 6, 8}
- F = {1, 2, 3, 4, 6, 12}
Элемент заказа и повторения
Элементы в наборе не обязательно должны быть в каком-то определенном порядке, поэтому вы также можете написать приведенный выше набор J как:
J = {Сатурн, Юпитер, Нептун, Уран}
или же
J = {Нептун, Юпитер, Уран, Сатурн}
Повторяющиеся элементы также не меняют набор, поэтому:
J = {Юпитер, Сатурн, Уран, Нептун}
а также
J = {Юпитер, Сатурн, Уран, Нептун, Юпитер, Сатурн}
один и тот же набор, потому что оба содержат только четыре разных элемента: Юпитер, Сатурн, Уран и Нептун.
Наборы и эллипсы
Если набор содержит бесконечное количество элементов, многоточие (…) выражает, что шаблон набора будет продолжаться вечно в этом направлении.
Например, набор целых чисел начинается с нуля, но не имеет конца, поэтому вы можете записать его как:
{0, 1, 2, 3, 4, 5, ...}
Другим специальным набором чисел, который не имеет конца, является набор целых чисел. Поскольку целые числа могут быть положительными или отрицательными, однако, набор использует эллипсы на обоих концах, чтобы показать, что набор продолжается вечно в обоих направлениях:
{..., −3, −2, −1, 0, 1, 2, 3, ...}
Другое использование для эллипсов — заполнить середину большого набора. Вы можете написать набор четных чисел от 0 до 100 как:
{0, 2, 4, 6, 8, ..., 94, 96, 98, 100}
Многоточие показывает, что шаблон — только четные числа — продолжается через неписанную часть набора.
Специальные наборы
Специальные наборы, которые часто используются, идентифицируются с использованием определенных букв или символов. Они включают:
- Ø или же {} — пустой набор — набор, не содержащий элементов
- U — универсальный набор — набор, содержащий все элементы, относящиеся к определению определенного набора
- Z — множество всех целых чисел, где Z знак равно…, −3, −2, −1, 0, 1, 2, 3, …}
- N — натуральные числа (положительные целые числа), где N = {1, 2, 3, 4, 5, …}
Реестр против описательных методов
Выписывание или перечисление элементов набора, таких как набор внутренних или земных планет в нашей солнечной системе, называется системной записью или методом реестра.
T = {ртуть, венера, земля, марс}
Другим вариантом для идентификации элементов набора является использование описательного метода, который использует краткое описание или имя для описания набора, например:
T = {земные планеты}
Нотация Set-Builder
Альтернативой реестровым и описательным методам является использование обозначения построителя множеств, которое представляет собой сокращенный метод, описывающий правило, которому следуют элементы набора (правило, которое делает их членами определенного набора).
Обозначение построителя множеств для множества натуральных чисел больше нуля:
{х | x ∈ N, x> 0}
или же
{x: x ∈ N, x> 0}
В нотации конструктора множеств буква «х» является заполнителем, который можно заменить любой другой буквой.
Сокращенные символы
Сокращенные символы, используемые в нотации компоновщика множеств, включают:
- Вертикальная черта или двоеточие (| или же : символы) — это разделители, читаемые как «такие,
- Строчные эпсилон (∈ символ) читается как «элемент»
- ∉ символ читается как «не элемент»
Итак, вы бы прочитали {х | x ∈ N, x> 0} as, «Множество всех x, таких, что x является элементом множества натуральных чисел, а x больше 0.»
Множества и диаграммы Венна
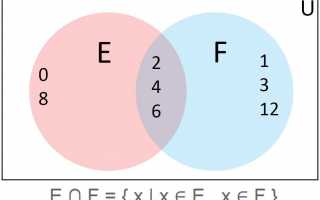
Диаграмма Венна (или набора) показывает отношения между элементами разных наборов. Перекрывающая часть диаграммы Венна показывает пересечение двух или более наборов (элементов, общих для обоих наборов).
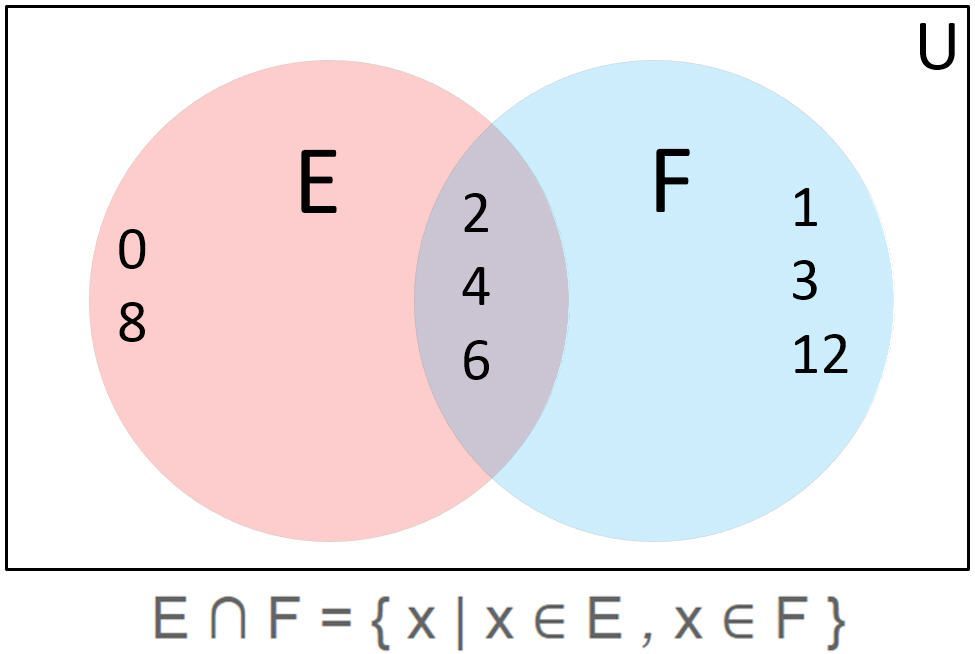
Обозначение построителя множества для операции (перевернутая буква «U» означает «пересечение»):
E ∩ F = {x | x ∈ E, x ∈ F}
Прямоугольная граница и буква U в углу диаграммы Венна, представленной выше, представляют собой универсальный набор всех рассматриваемых элементов для этой операции:
U = {0, 1, 2, 3, 4, 6, 8, 12}